04 Feb Análisis FEM dinámico de tensiones con de una raqueta y una bola

Este post muestra una análisis dinámico de tensiones mediante elementos finitos (FEM) poniendo como ejemplo la interacción entre una raqueta de tenis y una pelota. El ejemplo ilustra el contacto entre una superficie deformable y un conjunto de nodos, la definición de las tensiones iniciales y el modelado de una cavidad de fluido llena de un gas compresible utilizando la capacidad de la cavidad de fluido basada en la superficie.

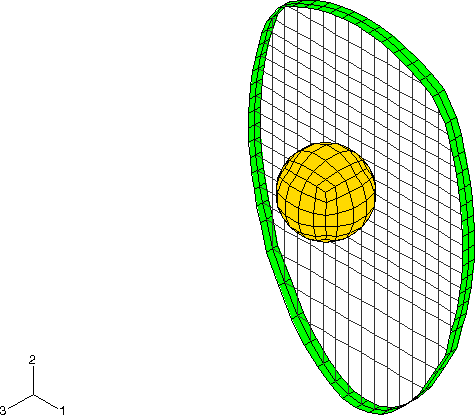
El ejemplo simula el impacto oblicuo de una pelota de tenis sobre una raqueta a 6.706 m/seg (264 in/seg).

El objetivo de éste ejemplo es mostrar cómo se puede llevar a cabo una análisis dinámico donde hay modelos rígidos y deformables, sujetos con presiones internas y utilizando elementos de linea (1D) y shell (2D). Éste ejemplo se puede extrapolar a otros escenarios de cualquier industria.

Modelado FEM de una raqueta de tenis

Los cordajes de la raqueta de tenis están modelados con los elementos Truss T3D2. Éste tipo de elementos Truss son elementos estructurales largos y delgados que pueden transmitir sólo la fuerza axial y no los momentos. Se supone que son elásticos y lineales, con un módulo de Young de 6.895 [GPa], un coeficiente de Poisson de 0.3, y una densidad de 1143 [kg/m3]. Las cuerdas están bajo una tensión inicial de 44.48 [N], la cual se especifica usando condiciones de tensión inicial.

Se supone que el marco es rígido y se modela usando elementos rígidos R3D4. Los elementos rígidos no son deformables, sin grados de libertad y siempre deben ser parte de un cuerpo rígido. Los nodos de las cuerdas (elementos Truss) alrededor del perímetro son los mismos nodos que los utilizados para los elementos R3D4. El nodo de referencia para el marco rígido tiene condiciones de contorno aplicados para restringir los seis grados de libertad en el cuerpo rígido de modo que el marco no se mueva.

Para más información sobre los diferentes tipos de elementos, revisa nuestro post Continuum, shell, beam y truss, ¿cuál utilizar?

Modelado FEM de un pelota de tenis

La pelota de tenis se modela como una esfera, usando 150 elementos shell S4R. Se supone que está hecha de goma, modelada con propiedades generales de material hiperelástico como un material Mooney-Rivlin con las constantes C10 = 0,690 [MPa] y C01 = 0,173 [MPa]. Abaqus/Explicit, el solver de Abaqus para análisis explícitos, requiere cierta compresibilidad para los materiales hiperelásticos. En los resultados mostrados aquí, D1= 0.0145 [MPa-1]. Esto da un módulo de volumen inicial (K0 = 2/D1) que es 80 veces el módulo de cortante inicial 2(C10+C01).

Esta relación es menor que la relación para cauchos típicos, pero los resultados no son particularmente sensibles a este valor en este caso porque el caucho no está conformado. Se necesitaría una representación más precisa de la compresibilidad del material si la goma estuviera conformada por componentes adyacentes o refuerzos más rígidos. La disminución de D1 en un orden de magnitud (por lo tanto, el aumento del módulo de volumen inicial por un factor de 10) tiene poco efecto en los resultados generales, pero causa una reducción en el incremento de tiempo estable por un factor de √10 debido al aumento del módulo de volumen, y ésto tiene un efecto en el tiempo de cálculo que es menor.

La densidad de la pelota de tenis es de 1068 [kg/m3].

La pelota de tenis está bajo una presión interna inicial de 41 [kPa] además de la presión atmosférica ambiente de 100 [kPa]. En el interior de la pelota de tenis se define una superficie basada en elementos. Esta superficie se utiliza para definir una cavidad llena de gas. Las propiedades del gas dentro de la pelota de tenis se definen como parte del comportamiento del fluido de una cavidad de fluido. El peso molecular y la capacidad calorífica molar del gas se eligen arbitrariamente como 0,062 [kg]  y 28,110 [J/kg °K]. Dado que la bola es impermeable al gas, la presión del gas aumentará cuando el volumen de la bola disminuya, y viceversa. El equilibrio estático da el valor de los esfuerzos iniciales de la membrana biaxial en los elementos del armazón de la esfera como pr/2t= 155 [kPa] para equilibrar la presión interna (aquí p es la presión interna del gas, r es el radio de la esfera, y t es el espesor de la pelota de tenis). Este estado inicial de tensión en la pelota se define en la simulación FEM usando condiciones de tensión iniciales.

Interacciones, cargas y condiciones de contorno de la raqueta y la bola

Se especifica un coeficiente de fricción de 0.1 entre la pelota y las cuerdas. La pelota impacta en las cuerdas a una velocidad de 6.706 [m/seg] con un ángulo de 15°.

No se ha intentado generar un modelo preciso de la pelota y las cuerdas: los parámetros del modelo se eligen simplemente para proporcionar una pelota «suave» en relación con las cuerdas para ilustrar los efectos de contacto. Hay 2241 grados de libertad en el modelo.

Para la interaccion entre las partes, se define una superficie basada en elementos en la pelota de tenis. Como los elementos Truss son elementos de línea, no forman una superficie plana. Se define una superficie basada en nodos que contiene todos los nodos de las cuerdas. Los pares de contacto se utilizan para definir el contacto entre la superficie basada en elementos de la pelota y cualquiera de los nodos definidos en la superficie basada en nodos.

Resultados

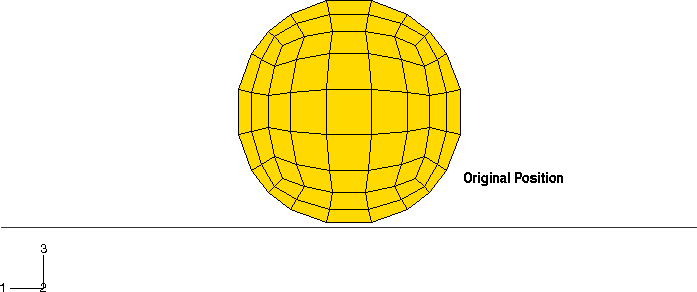
La imagen muestra la posición de la bola con respecto a las cuerdas en la configuración no deformada.

Las formas deformadas en las diferentes etapas del análisis se muestran en las siguiente imágenes.

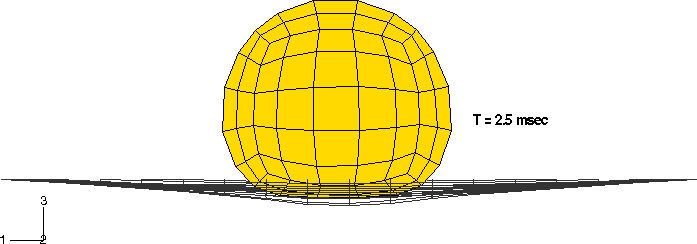
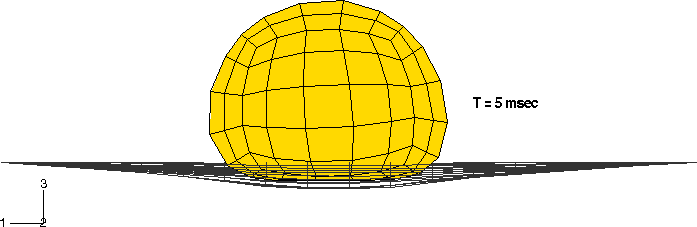
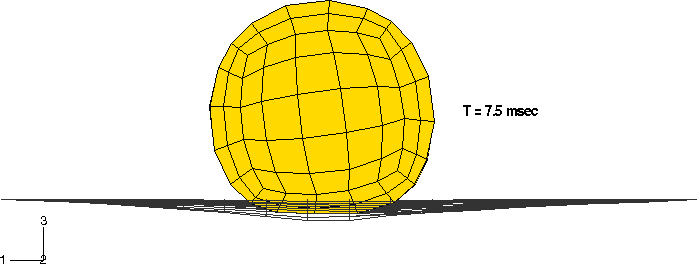
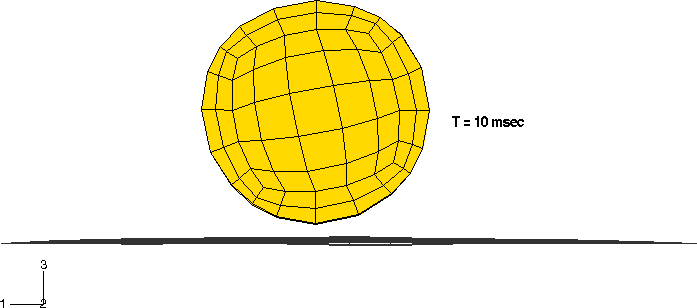
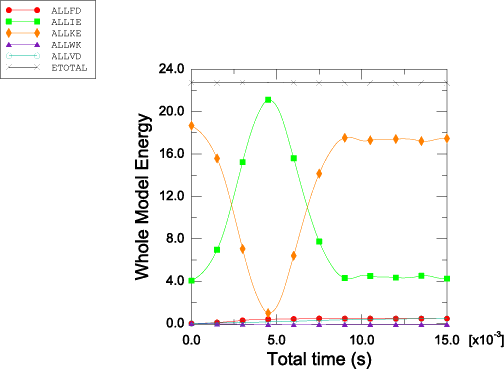
También se  muestra una historia temporal de las energías para el modelo. Estas incluyen la energía total interna (ALLIE), la energía cinética (ALLKE), la disipación viscosa (ALLVD), la energía disipada por fricción (ALLFD), el trabajo externo (ALLWK), y el balance de energía total para el modelo (ETOTAL). Se observa que la energía total permanece casi constante durante el análisis, como debería ser.

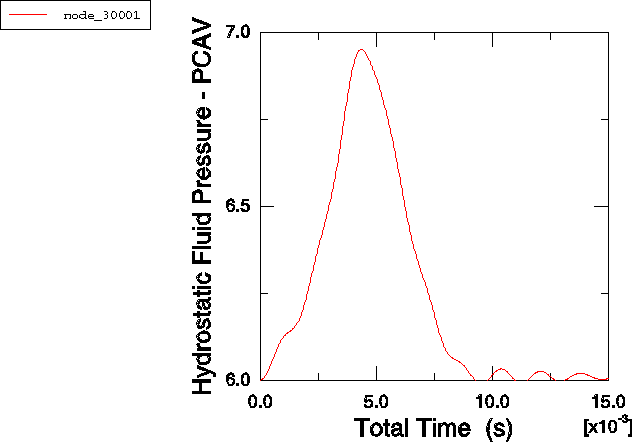
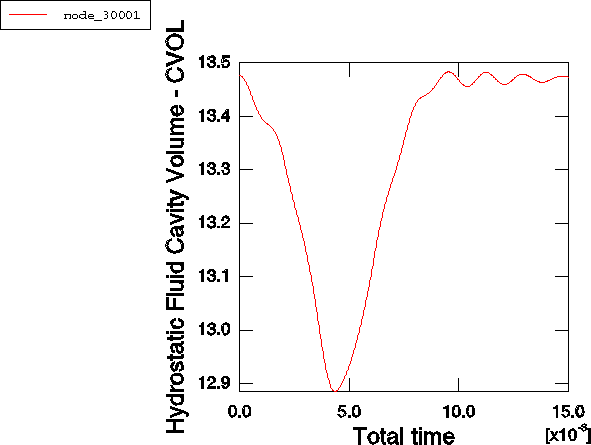
Por último, se da la historia de la presión dentro del balón y la historia del volumen real del balón. Se puede ver que tanto la presión del gas dentro de la bola como el volumen de la bola se estabilizan después de 10 mseg.

Én el siguiente video se puede ver una animacion de la simulacion de tensiones FEM con la raqueta de tenis y una bola

Referencias:

• Tennis racket and ball from the Abaqus Example Problems Guide

Pónte en contacto con contacto@4realsim.com para obtener más información sobre los servicios de Abaqus y/o FEA.